O objetivo desse post é passar rapidamente por um fluxo de trabalho usando o {tidymodels} para executar uma regressão logística, comparando-a rapidamente com outro modelo. Não abordei a seleção de features ou a interpretação dos coeficientes, nem realizei uma análise exploratória dos dados.

O {tidymodels} compreende um workflow muito prático para trabalhar com modelagem, sendo relativamente simples analisar a performance e comparar diferentes modelos.

Aqui estou apenas raspando a superfície do que é possível fazer e recomendo fortemente a leitura do livro Tidy modelling with R, que além de excelente para explicar o framework em si, também cumpre a função de pincelar diversos conceitos importantes de modelagem.

Leitura dos dados

Primeiro vou carregar as dependências necessárias para a análise. Aqui vou usar principalmente dois conjuntos de pacotes, o {tidyverse} e o {tidymodels}. Adicionalmente, estou usando o pacote {conflicted}, para lidar com conflitos entre algumas dependências:

library(tidymodels)
library(tidyverse) 
library(conflicted)

Em seguida leio a tabela, que também está disponível aqui e trato minimamente as variáveis:

conflict_prefer("spec", "yardstick") # resolvendo conflitos de pacotes
tidymodels::tidymodels_prefer() # preferindo funções do tidymodels

# leitura da tabela
  # converti algumas colunas para fator
  # omiti os NA
df_heart <- 
  read.csv("https://www.dropbox.com/s/t1158k6mghefmmn/framingham.csv?dl=1") %>% 
  mutate_at(c("male","education","currentSmoker", 
              "prevalentStroke","prevalentHyp","diabetes",
              "TenYearCHD"), as.factor) %>% 
  na.omit()

Com isso tenho uma tabela com as variáveis abaixo:

glimpse(df_heart)

## Rows: 3,656
## Columns: 16
## $ male            <fct> 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, ~
## $ age             <int> 39, 46, 48, 61, 46, 43, 63, 45, 52, 43, 50, 43, 46, 41~
## $ education       <fct> 4, 2, 1, 3, 3, 2, 1, 2, 1, 1, 1, 2, 1, 3, 2, 3, 2, 2, ~
## $ currentSmoker   <fct> 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, ~
## $ cigsPerDay      <int> 0, 0, 20, 30, 23, 0, 0, 20, 0, 30, 0, 0, 15, 0, 20, 10~
## $ BPMeds          <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, ~
## $ prevalentStroke <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ~
## $ prevalentHyp    <fct> 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, ~
## $ diabetes        <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ~
## $ totChol         <int> 195, 250, 245, 225, 285, 228, 205, 313, 260, 225, 254,~
## $ sysBP           <dbl> 106.0, 121.0, 127.5, 150.0, 130.0, 180.0, 138.0, 100.0~
## $ diaBP           <dbl> 70.0, 81.0, 80.0, 95.0, 84.0, 110.0, 71.0, 71.0, 89.0,~
## $ BMI             <dbl> 26.97, 28.73, 25.34, 28.58, 23.10, 30.30, 33.11, 21.68~
## $ heartRate       <int> 80, 95, 75, 65, 85, 77, 60, 79, 76, 93, 75, 72, 98, 65~
## $ glucose         <int> 77, 76, 70, 103, 85, 99, 85, 78, 79, 88, 76, 61, 64, 8~
## $ TenYearCHD      <fct> 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, ~

Estes dados se referem à dados coletados de pacientes em um estudo que procura entender que fatores podem estar ligados à problemas cardíacos futuros (mais detalhes na página do Kaggle referente a este dataset). A variável de resposta nesse caso vai ser a coluna TenYearCHD.

Partições de treino, teste & replicatas

A primeira coisa a ser feita é particionar os dados. Basicamente quero três conjuntos de dados:

1. Um conjunto de dados de treino.
2. Um conjunto de dados de teste.
3. Um conjunto de replicatas para testar a performance do modelo.

Para executar os primeiros dois passos acima, vou utilizar as funções abaixo:

set.seed(123)

heart_split <- 
  initial_split(df_heart, prop = 0.80)  

A função initial_split cria uma variável que armazena informações sobre as partições de treino, teste e conjunto completo de dados, a partir da tabela df_heart. O argumento prop indica em que proporção minha tabela original será particionada.

O tamanho de cada partição podem ser conferidos chamando a variável:

heart_split

## <Analysis/Assess/Total>
## <2924/732/3656>

Desta variável, extraio as tabelas de treino e teste executando as funções abaixo:

heart_train <- training(heart_split)

heart_test  <-  testing(heart_split)

A variável heart_train contém os dados de teste, que compõe 80% do total da amostra. O restante encontra-se na variável heart_test. Toda essa separação ajuda a evitar o vazamento de dados de modelagem entre as partições, o que prejudicaria o processo.
Por último, vou criar um conjunto de dados com replicatas dos dados de treino, reamostrados entre si:

set.seed(123)
heart_folds <- vfold_cv(heart_train)

No caso acima utilizei uma validação cruzada para criar as replicatas.

Estas serão utilizadas para testar a performance do modelo ajustado.

Criando receitas

Agora é hora de criar a “receita” da modelagem. Isso envolve basicamente definir qual será a fórmula utilizada na regressão bem como qualquer ajuste a mais que deva ser feitos nos dados:

heart_recipe <- 
recipe(TenYearCHD ~ male + age + cigsPerDay + prevalentStroke + 
         prevalentHyp + totChol + sysBP + glucose,
       data = heart_train) %>% 
  step_center(all_numeric_predictors()) %>% 
  themis::step_downsample(TenYearCHD)

Esta é uma etapa onde muito ajuste fino pode ser feito. Acima fiz apenas o básico: defini a variáveis de resposta e explicativas e indiquei que todas variáveis descritivas que sejam numéricas deveriam ser centralizadas. Além disso, eu indiquei que deveria ser feito o downsampling nos dados a partir de minha variável de resposta, uma vez que meus dados apresentam desbalanço de classes.

Seguida a esta etapa, defino qual tipo de modelo irei utilizar, neste caso, uma regressão logística:

modelo_log <- 
  logistic_reg() %>% 
  set_engine("glm") %>% 
  set_mode("classification")

Só para deixar as coisas mais interessantes, posso criar uma variável que contém especificações de outro tipo de modelo, como as de uma árvore de decisão:

modelo_dtree <- 
  decision_tree() %>% 
  set_engine("rpart") %>% 
  set_mode("classification")

Dessa maneira, eu posso conferir a performance de cada um dos dois modelos usando a fórmula criada.

Antes de prosseguir, vou definir uma variável que vai servir de argumento para armazenar as previsões feitas nas replicatas:

control <- control_resamples(save_pred = TRUE)

A ideia de usar as replicatas é, em parte, entender como as métricas de performance variam quando ajustamos o modelo em cada uma:

heart_resamples_preds <- 
  fit_resamples(modelo_log, 
                heart_recipe, 
                heart_folds, 
                control = control)

O que o código acima faz é o seguinte:

1. Define qual modelo será ajustado
2. Implementa as instruções da receita (fórmula + centralização, no nosso caso)
3. Aplica estas etapas nas replicatas, salvando as previsões em tabelas.

A variável heart_resamples_preds contém as informações dos ajustes de cada replicata e, sendo assim, posso extrair uma média das métricas de performance de cada ajuste:

collect_metrics(heart_resamples_preds)

## # A tibble: 2 x 6
##   .metric  .estimator  mean     n std_err .config             
##   <chr>    <chr>      <dbl> <int>   <dbl> <chr>               
## 1 accuracy binary     0.660    10 0.00815 Preprocessor1_Model1
## 2 roc_auc  binary     0.724    10 0.0151  Preprocessor1_Model1

Na tabela acima, está estimada a acurácia e AUC médias dos ajustes das 10 replicatas acima.

Aqui o interessante é que a sintaxe do tidymodels me permite extrair estas mesmas informações a partir de outro modelo. Dado que criei a variável modelo_dtree, que contém as especificações da árvore de decisões, posso substituir apenas o argumento referente ao modelo sendo ajustado no código e extrair as métricas para este outro algoritmo:

heart_resamples_preds_dtree <- 
  fit_resamples(modelo_dtree, 
                heart_recipe, 
                heart_folds, 
                control = control)

collect_metrics(heart_resamples_preds_dtree)

## # A tibble: 2 x 6
##   .metric  .estimator  mean     n std_err .config             
##   <chr>    <chr>      <dbl> <int>   <dbl> <chr>               
## 1 accuracy binary     0.636    10  0.0101 Preprocessor1_Model1
## 2 roc_auc  binary     0.663    10  0.0171 Preprocessor1_Model1

A acurácia foi semelhante à regressão logística, mas a AUC foi bastante inferior. Isto me daria informação o suficiente para prosseguir com a regressão logística em detrimento à árvore de decisões.

O potencial que esta lógica e sintaxe carrega estao no fato de que eu poderia iterativamente testar a performance de \(n\) modelos com os mesmos dados, tratamentos e fórmulas, de maneira bastante simples. Eu poderia, inclusive, testar modelos com fórmulas diferentes, mas isto é tema para outra postagem.

Neste caso específico seguirei com a regressão logística (até porque as métricas parecem indicar que este é o melhor caminho).

Após analisar a AUC das replicatas, o próximo passo é ajustar o modelo na partição de treino, antes disso porém, vou dar uma olhada na curva ROC referente às replicatas:

augment(heart_resamples_preds) %>%
  roc_curve(TenYearCHD, .pred_0) %>%
  autoplot()

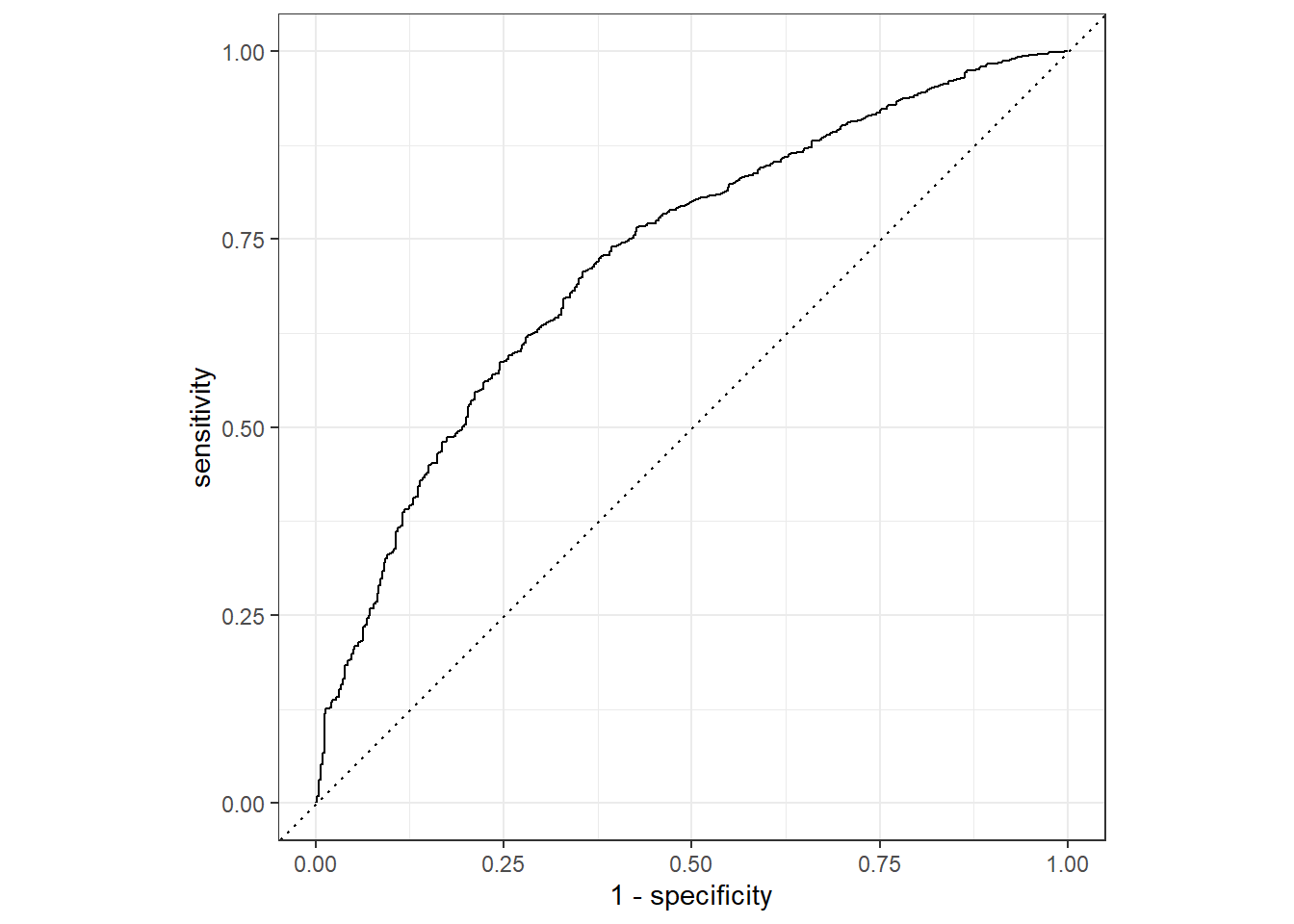
As funções utilizadas acima facilitam a plotagem da curva. Um fato interessante é que o objeto que gera o gráfico é um ggplot e, sendo assim, podemos manipular ele normalmente:

augment(heart_resamples_preds) %>%
  roc_curve(TenYearCHD, .pred_0) %>%
  autoplot() +
  ggtitle("Curva ROC") # adicionando título

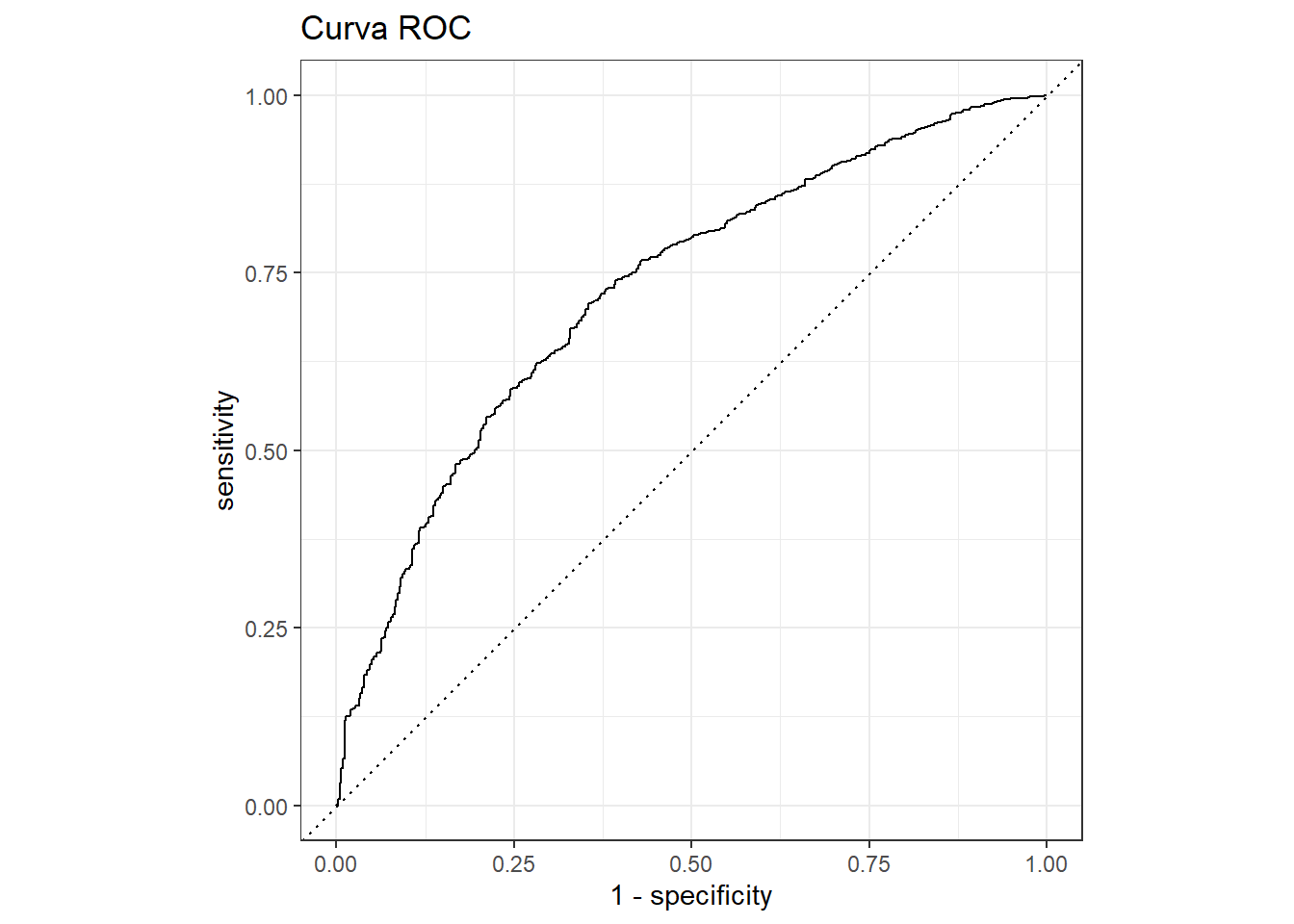
Caso eu quisesse fazer ainda mais ajustes na curva, eu poderia usar o output parcial do código, que gera a tabela utilizada para fazer o plot, que contém os valores de especificidade e sensibilidade:

augment(heart_resamples_preds) %>%
  roc_curve(TenYearCHD, .pred_0)

## # A tibble: 2,926 x 3
##    .threshold specificity sensitivity
##         <dbl>       <dbl>       <dbl>
##  1 -Inf           0             1    
##  2    2.29e-7     0             1    
##  3    3.31e-7     0.00227       1    
##  4    3.70e-7     0.00455       1    
##  5    3.72e-7     0.00455       1.00 
##  6    8.25e-7     0.00455       0.999
##  7    3.23e-2     0.00455       0.999
##  8    4.22e-2     0.00682       0.999
##  9    4.88e-2     0.00909       0.999
## 10    5.79e-2     0.0114        0.999
## # ... with 2,916 more rows

Agora, seguirei os mesmos passos acima, mas dessa vez ajustando o modelo à partição de treino:

heart_wflow_fit <- 
  workflow() %>% 
  add_model(modelo_log) %>% 
  add_recipe(heart_recipe) %>% 
  fit(heart_train)

A partir deste ajuste, vou realizar as previsões na partição de teste. Abaixo estou executando a função predict duas vezes: uma para coletar os outputs na forma de classes e outra na forma de probabilidades:

df_predictions_test <- 
  heart_test %>% 
  select(TenYearCHD) %>% 
  bind_cols( 
    predict(heart_wflow_fit, heart_test, type = "prob"), # output como probs
    predict(heart_wflow_fit, heart_test) # output como classes
  )

Vou dar uma conferida em diferentes métricas dessa vez, além da acurácia. Eu posso fazer isso criando uma lista de métricas usando a função metric_set, especificando como argumentos as métricas que quero extrair e, em seguida, usando a função custom_metrics, para gerar o output:

custom_metrics <- 
  metric_set(accuracy, sens, spec, precision, 
             recall, f_meas, kap, mcc)

custom_metrics(df_predictions_test,
               truth = TenYearCHD,
               estimate = .pred_class)

## # A tibble: 8 x 3
##   .metric   .estimator .estimate
##   <chr>     <chr>          <dbl>
## 1 accuracy  binary         0.649
## 2 sens      binary         0.631
## 3 spec      binary         0.744
## 4 precision binary         0.928
## 5 recall    binary         0.631
## 6 f_meas    binary         0.751
## 7 kap       binary         0.223
## 8 mcc       binary         0.277

Abaixo, o valor de AUC e a curva ROC:

roc_auc(df_predictions_test, truth = TenYearCHD,
        estimate = .pred_0)

## # A tibble: 1 x 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 roc_auc binary         0.752

df_predictions_test %>%
  roc_curve(truth = TenYearCHD, .pred_0) %>%
  autoplot()

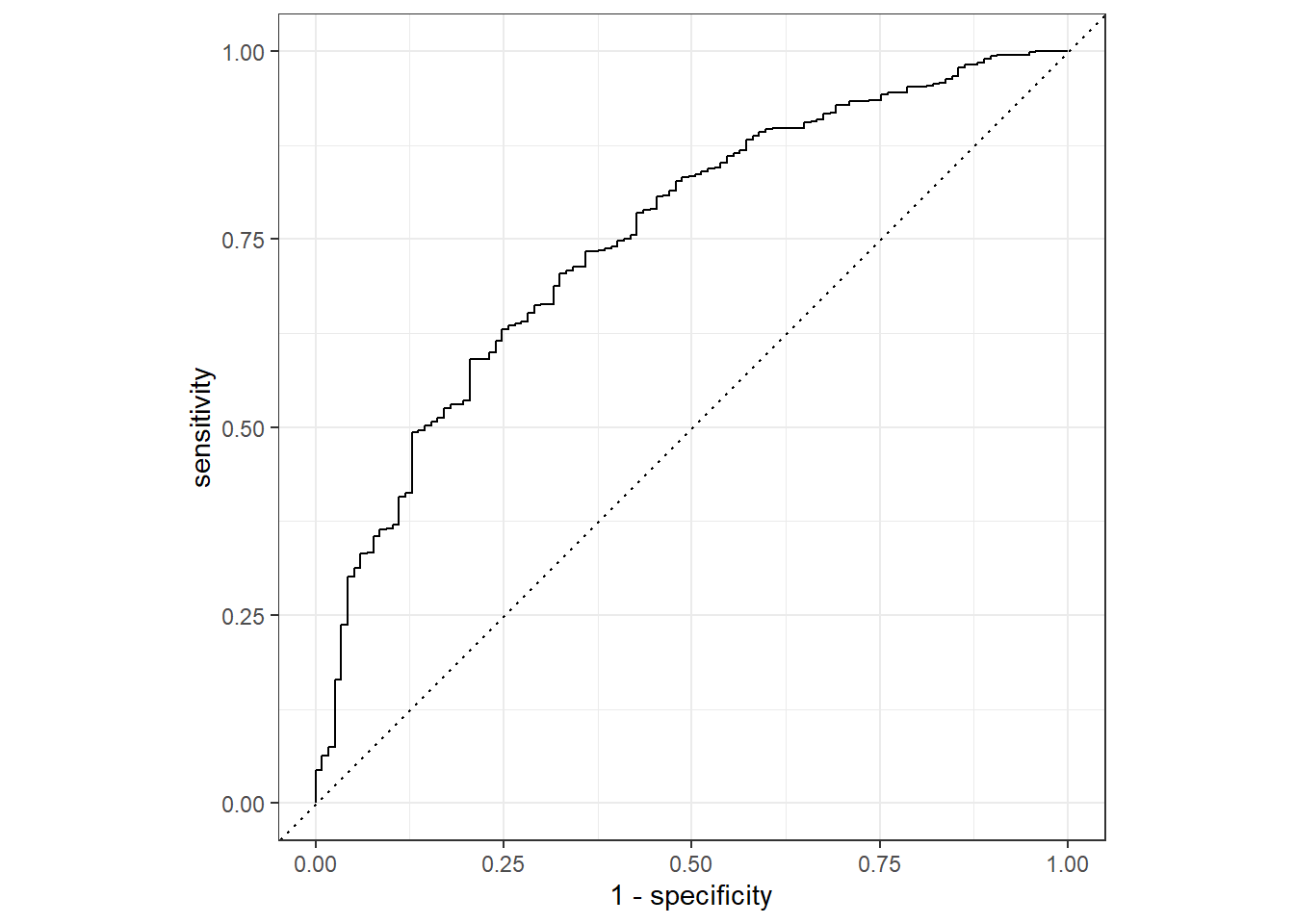
Finalmente, vou conferir os valores dos coeficientes associados ao meu modelo. Posso deixar o output mais amigável e já exponenciado usando a função tidy com o argumento exponentiate = TRUE, aproveitei para deixar a tabela na ordem decrescente de estimativas e filtrei por valores significativos de p:

heart_wflow_fit %>% 
  tidy(exponentiate = TRUE) %>% 
  arrange(desc(estimate)) %>% 
  filter(p.value < 0.05)

## # A tibble: 6 x 5
##   term        estimate std.error statistic       p.value
##   <chr>          <dbl>     <dbl>     <dbl>         <dbl>
## 1 male1          1.65    0.159        3.17 0.00154      
## 2 age            1.06    0.00957      6.04 0.00000000155
## 3 cigsPerDay     1.02    0.00681      2.99 0.00278      
## 4 sysBP          1.01    0.00444      2.52 0.0118       
## 5 totChol        1.00    0.00170      2.45 0.0145       
## 6 (Intercept)    0.556   0.129       -4.53 0.00000578

Conclusões

Tenho me animado recentemente com o uso do {tidymodels} e a motivação deste post foi compartilhar um pouco do porque esse fluxo é interessante e como ele pode aumentar a produtividade na hora de desenvolver modelos.

Abaixo alguns motivos para isso:

1. O {tidymodels} tem uma boa interface com a sintaxe do {tidyverse}, o que significa um código mais limpo, intepretável, intuititivo e de alto nível.

2. As funções já existentes no framework nos permite executar processos com bastante facilidade, sem ter que produzir código específico para isso. No post acima, por exemplo, foi demonstrado como é possível rapidamente comparar a performance de outros modelos com os mesmos dados ou analisar a performance do modelo a partir de replicatas.

3. Interpretar e extrair os resultados das modelagens (valores das previsões e coeficientes, por exemplo) é simples e, em geral, feito de maneira tabular, o que permite uma fácil manipulação dos dados.

4. Fácil plotar a curva ROC!

Existem muitas outras vantagens em se usar esse framework, como o fácil acesso às bibliotecas mais populares de machine learning. Além disso, a estrutura de como o fluxo funciona estimula o uso de boas práticas de modelagem.