Regressão Linear Simples - Fish Market data
By Lucas Moraes in Regressão linear Distância de Cook vif
January 1, 0001
Esta é uma pequena análise de regressão linear usando R. Meu objetivo aqui foi revisitar alguns conceitos, criar algumas funções e visualizar alguns dados referentes ao tema.
Vou usar o dataset
Fish quem contém diferentes medidas corporais de peixes registrados em um mercado. Este foi retirado do kaggle e armazenado no meu dropbox, para posteridade. Todo código utilizado para gerar essa análise está disponível no
repo do projeto, em meu github pessoal.
Antes, entretanto, de prosseguir, existe uma pergunta fundamental a ser respondida: porque e quando usar uma regressão linear? A grosso modo, ela pode ser utilizada para estimar um determinado valor (um valor esperado), com base em outro. Nesse contexto, assume-se que a relação entre estes dados é uma função linear.
Explorando o dataset e suas variáveis
O primeiro passo, como sempre, é se familiarizar com o dataset e carregar os pacotes que vou utilizar:
## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.0 ──
## ✓ ggplot2 3.3.5 ✓ purrr 0.3.4
## ✓ tibble 3.1.3 ✓ dplyr 1.0.7
## ✓ tidyr 1.1.3 ✓ stringr 1.4.0
## ✓ readr 1.4.0 ✓ forcats 0.5.1
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag() masks stats::lag()
## Loading required package: carData
##
## Attaching package: 'car'
## The following object is masked from 'package:dplyr':
##
## recode
## The following object is masked from 'package:purrr':
##
## some
##
## ── Column specification ────────────────────────────────────────────────────────
## cols(
## Species = col_character(),
## Weight = col_double(),
## Length1 = col_double(),
## Length2 = col_double(),
## Length3 = col_double(),
## Height = col_double(),
## Width = col_double()
## )
Species <chr> | Weight <dbl> | Length1 <dbl> | Length2 <dbl> | Length3 <dbl> | Height <dbl> | Width <dbl> |
|---|---|---|---|---|---|---|
| Bream | 242.0 | 23.2 | 25.4 | 30.0 | 11.5200 | 4.0200 |
| Bream | 290.0 | 24.0 | 26.3 | 31.2 | 12.4800 | 4.3056 |
| Bream | 340.0 | 23.9 | 26.5 | 31.1 | 12.3778 | 4.6961 |
| Bream | 363.0 | 26.3 | 29.0 | 33.5 | 12.7300 | 4.4555 |
| Bream | 430.0 | 26.5 | 29.0 | 34.0 | 12.4440 | 5.1340 |
| Bream | 450.0 | 26.8 | 29.7 | 34.7 | 13.6024 | 4.9274 |
| Bream | 500.0 | 26.8 | 29.7 | 34.5 | 14.1795 | 5.2785 |
| Bream | 390.0 | 27.6 | 30.0 | 35.0 | 12.6700 | 4.6900 |
| Bream | 450.0 | 27.6 | 30.0 | 35.1 | 14.0049 | 4.8438 |
| Bream | 500.0 | 28.5 | 30.7 | 36.2 | 14.2266 | 4.9594 |
Os nomes das colunas não são lá muito intuitivos, por isso os descrevo abaixo:
Species: nome da espécie mensurada.Weight: Peso do peixe em gramas.Length1: comprimento vertical em cm.Length2: comprimento diagonal em cm.Length3: comprimento cruzado em cm.Height: altura em cm.Width: largura diagonal em cm.
Meu objetivo aqui vai ser usar o peso como variável de resposta ou seja, quero usar alguma(s) das demais variáveis para prever qual vai ser o peso do peixe, o que, por sua vez, vai indicar (a grosso modo) seu porte.
Como pontapé inicial, vou plotar o peso em função de cada uma das demais variáveis, isso vai me dar uma visão geral dessas correlações:
Para plotar tudo de uma vez alterei um pouco a tabela e criei um grid:
## `geom_smooth()` using formula 'y ~ x'

É possível perceber que a correlação do peso com as demais medidas é positiva em todos casos, pela inclinação das retas de regressão (tracejadas azuis), em alguns mais e outros menos. Entretanto, fica difícil entender a robustez dos modelos visualmente. Sendo assim, vou computar esses valores, na forma de R2, em uma tabela e ordenar de maneira decrescente:
## # A tibble: 5 × 2
## variables r_squared
## <chr> <dbl>
## 1 Length3 0.852
## 2 Length2 0.844
## 3 Length1 0.839
## 4 Width 0.786
## 5 Height 0.525
Essa tabela me dá os valores de \(R^2\) entre o peso e cada uma das outras variáveis independentemente (não sendo covariáveis) para cada modelo simples .
Seguindo por essa lógica, as três medidas de comprimento são as que melhor descrevem o comportamento do peso. Ainda, a natureza semelhante dessas medidas nos leva a crer que possivelmente existe uma colinearidade nessa relação.
Vou desenvolver isso um pouco mais a frente, mas por hora, como vou fazer uma regressão simples, vou usar a variável Length3 como explanatória, dado que ela resultou no maior valor de \(R^2\).
Abaixo, os coeficientes do modelo:
##
## Call:
## lm(formula = Weight ~ Length3, data = fish)
##
## Coefficients:
## (Intercept) Length3
## -490.40 28.46
Segundo esse modelo, existe um incremento de cerca de 28 gramas no peso de um peixe conforme a largura cruzada do peixe aumenta em uma unidade, ou seja, 1 centímetro.
Abaixo, vou plotar o gráfico da regressão, já atribuindo cores diferentes aos pontos referenes a cada espécies da amostra (estou levando todas em consideração):
A qualidade da regressão
## `geom_smooth()` using formula 'y ~ x'
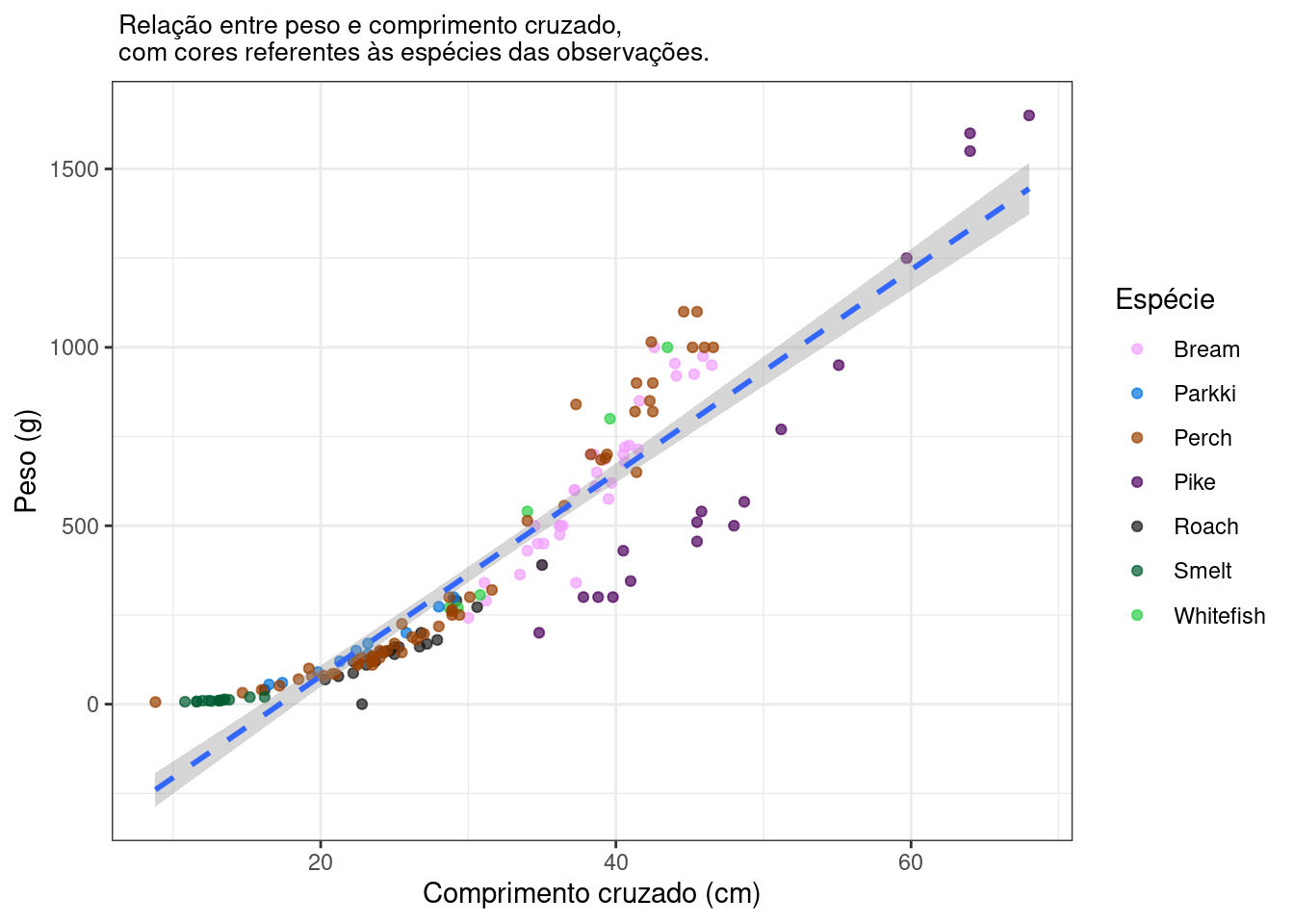
Um fator interessante de se notar é a provável alta influência dos pontos associados à espécie Pike (em roxo), na inclinação e erro associado da reta, devido ao alto valor tanto de peso quanto de comprimento cruzado de alguns de seus pontos. Essa espécie provavelmente tem maiores valores, em média, de distância de cook para suas observações, o que vai influenciar no comportamento da reta. Podemos checar isso sumarizando o modelo e esses valores, por espécie:
## # A tibble: 7 × 2
## Species mean_cooksd
## <fct> <dbl>
## 1 Pike 0.0428
## 2 Smelt 0.0116
## 3 Whitefish 0.00550
## 4 Perch 0.00528
## 5 Bream 0.00325
## 6 Roach 0.00150
## 7 Parkki 0.000504
A distância de Cook mede a influência das observações na inclinação e erro associado à reta de regressão, ou, seja, a influência destes nos valores ajustados: quanto maior esse valor, mais a inclinação da reta e seu erro está sendo definido por essas observações.
Como previsto, a espécie Pike de fato tem a maior média para os valores de distância de Cook associada a seus pontos, seguida pela espécie Smelt (verde escuro), que no gráfico tem uma concentração de pontos, relativamente alta, próximos de zero. Esses pontos, em ambas espécies, se distanciam bastante da reta de regressão, explicando o comportamento das médias de distância de Cook associadas a elas.
Vou checar mais a fundo a influência destas espécies na reta e no valor de \(R^2\).
Lembrando que o modelo tem \(R^2\) de 0.85, vou verificar qual valor que \(R^2\) assume retirando essas espécies dele:
## [1] 0.9109848
Retirando as espécies, a robustez do modelo aumenta significativamente. A inclinação da reta também se altera, conforme podemos ver na mudança do coeficiente associado à variável explanatória de comprimento cruzado:
##
## Call:
## lm(formula = Weight ~ Length3, data = .)
##
## Coefficients:
## (Intercept) Length3
## -656.48 34.14
Para enxergar essa alteração melhor ainda, podemos sobrepor as retas de cada modelo:
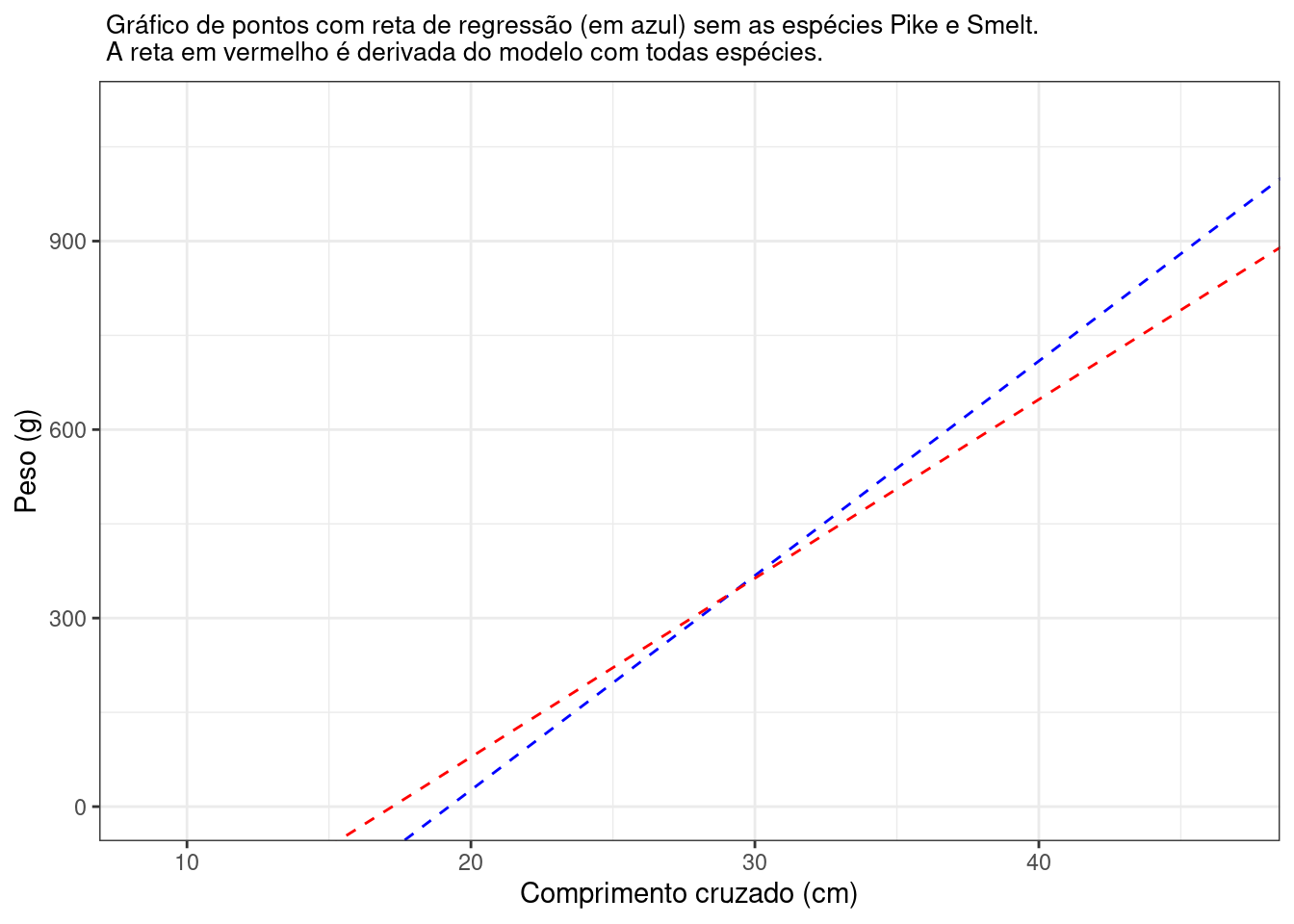 Visualizando dessa forma fica mais claro o comportamento da nova reta em comparação com a reta associada ao primeiro modelo (tracejada vermelha). Essa inclinação indica uma correlação mais forte entre as variáveis na ausência das espécies Pike e Smelt, fato reforçado quando se calcula os índices de pearson para os dois casos:
Visualizando dessa forma fica mais claro o comportamento da nova reta em comparação com a reta associada ao primeiro modelo (tracejada vermelha). Essa inclinação indica uma correlação mais forte entre as variáveis na ausência das espécies Pike e Smelt, fato reforçado quando se calcula os índices de pearson para os dois casos:
## # A tibble: 2 × 2
## df indice_pearson
## <chr> <dbl>
## 1 df_original 0.923
## 2 df_sem_especies_ruido 0.954
Finalmente, sem aprofundar muito, existe outra maneira prática de verificar o quanto os pontos das espécies podem estar influenciando na qualidade da regressão, que é plotando as curvas de regressão por espécie:
## `geom_smooth()` using formula 'y ~ x'
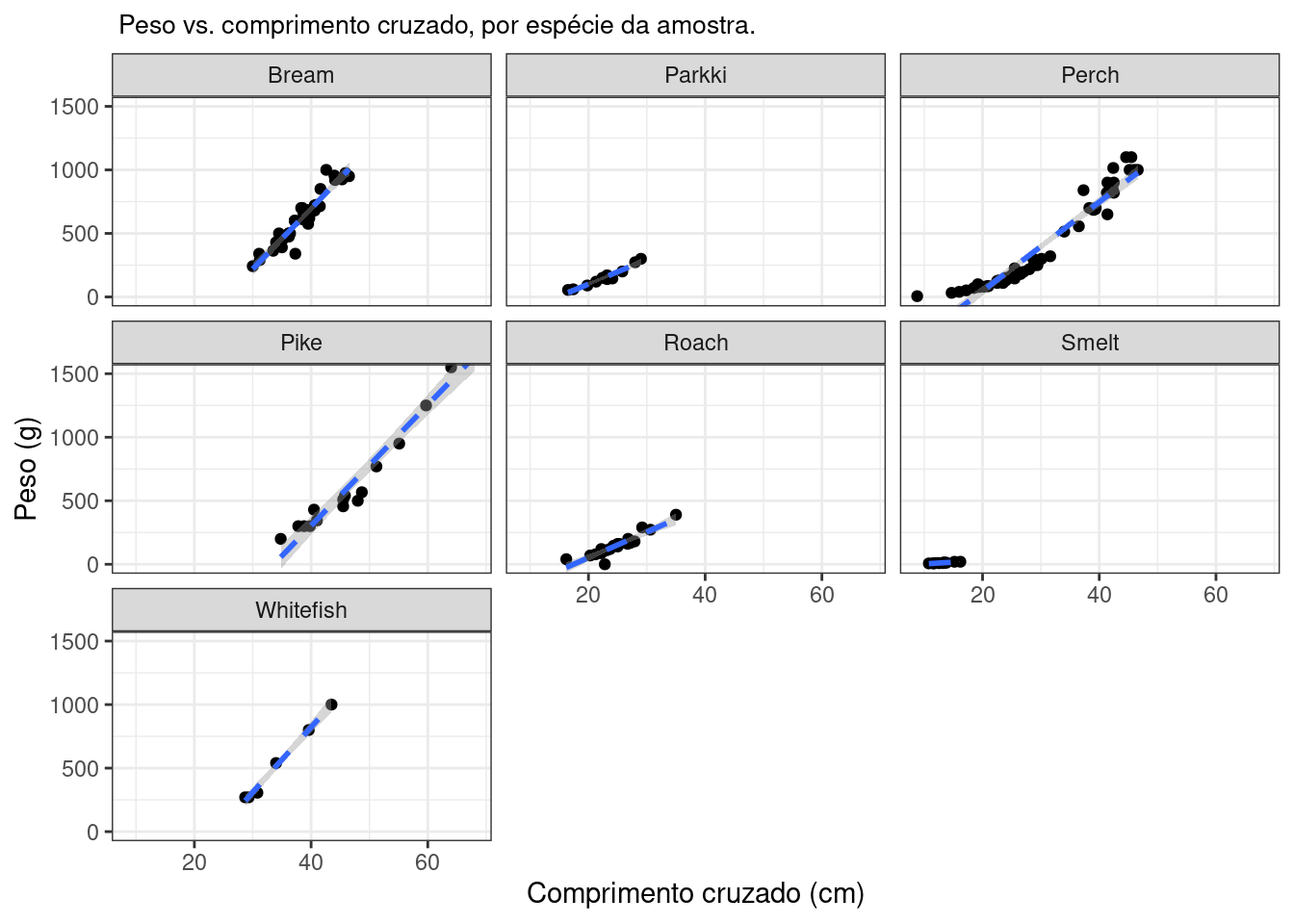
A espécie Pike é a única com valores de peso maiores que 1500. Já a espécie Smelt tem apenas valores próximos de zero, reforçando um pouco da influência destas na qualidade da regressão. Essa informação é redundante com o gráfico onde os pontos foram pintados de acordo com as espécies de referência, mas é uma maneira distinta interessante de enxergar esse comportamento.
Esse tipo de fator levanta a questão: quais espécies escolher para estabelecer um modelo geral? Uma maneira de fazer isso seria calculando o \(R^2\) associado ao modelo escolhido por espécie, mas também indicando o número de observações por espécie que existe nos dados:
## # A tibble: 5 × 2
## variables r_squared
## <chr> <dbl>
## 1 Length3 0.852
## 2 Length2 0.844
## 3 Length1 0.839
## 4 Width 0.786
## 5 Height 0.525
## # A tibble: 7 × 4
## Species variables r_squared n
## <fct> <chr> <dbl> <int>
## 1 Whitefish Length3 0.993 6
## 2 Pike Length3 0.958 17
## 3 Parkki Length3 0.943 11
## 4 Perch Length3 0.921 56
## 5 Smelt Length3 0.898 14
## 6 Bream Length3 0.897 35
## 7 Roach Length3 0.842 20
Quando analisadas em separado, a espécie Pike (que apresentava altos valores de distância cook, em média), não apresenta um \(R^2\) tão baixo. Mas é importante observar que o número de observações da maior parte das espécies da amostra é bem baixo (menor que 20). Apenas as espécies Perch e Bream tem mais de 20 observações. A espécie Whitefish, que contém o maior valor de \(R^2\) em seu modelo, contém apenas 6 observações. Se a ideia fossse utilizar um modelo generalista, seria razoável manter apenas espécies número alto de observações (20 talvez) ou aumentar o número de medidas das espécies subamostradas.
Colinearidade de variáveis
Como observado, todas medidas de comprimento apresentaram altos valores de \(R^2\) quando correlacionados com o peso. Recapitulando a tabela:
## # A tibble: 5 × 2
## variables r_squared
## <chr> <dbl>
## 1 Length3 0.852
## 2 Length2 0.844
## 3 Length1 0.839
## 4 Width 0.786
## 5 Height 0.525
Esse comportamento pode ser um indicativo de colinearidade, o que faria sentido dada a natureza similar dessas medidas, em termos de proporção. Isso pode ser conferido computando os fatores de inflação de variância (Vif) para cada variável, em um modelo que leva em conta todas variáveis:
## Length1 Length2 Length3 Height Width
## 1681.49649 2084.25783 422.46825 14.57009 12.27536
Os altos valores de VIF para as medidas de comprimento indicam que essas variáveis são, de fato, redundantes para o modelo, não fazendo diferença qual é utilizada: ambas tem boa perfomance para explicar os valores de peso. Explicando superficialmente, o Vif indica a severidade da colinearidade de variáveis.
Esse comportamento pode ser visualizado se plotarmos, por exemplo, o peso em função de dois comprimentos quaisquer:
##
## Attaching package: 'plotly'
## The following object is masked from 'package:ggplot2':
##
## last_plot
## The following object is masked from 'package:stats':
##
## filter
## The following object is masked from 'package:graphics':
##
## layout
## Warning: 'scatter3d' objects don't have these attributes: 'colorbar'
## Valid attributes include:
## 'type', 'visible', 'showlegend', 'legendgroup', 'opacity', 'name', 'uid', 'ids', 'customdata', 'meta', 'hoverlabel', 'stream', 'transforms', 'uirevision', 'x', 'y', 'z', 'text', 'texttemplate', 'hovertext', 'hovertemplate', 'mode', 'surfaceaxis', 'surfacecolor', 'projection', 'connectgaps', 'line', 'marker', 'textposition', 'textfont', 'hoverinfo', 'error_x', 'error_y', 'error_z', 'xcalendar', 'ycalendar', 'zcalendar', 'scene', 'idssrc', 'customdatasrc', 'metasrc', 'xsrc', 'ysrc', 'zsrc', 'textsrc', 'texttemplatesrc', 'hovertextsrc', 'hovertemplatesrc', 'textpositionsrc', 'hoverinfosrc', 'key', 'set', 'frame', 'transforms', '_isNestedKey', '_isSimpleKey', '_isGraticule', '_bbox'
Os pontos se dispersam muito pouco, o que indica sobreposição dos mesmos e sua redundância. Caso essa colinearidade não existisse, não seria esperada uma “quase reta” dentro de um espaço tridimensional.
Conclusões
No geral, a primeira conclusão que pode ser tirada da análise, é que o comprimento é a medida que melhor descreve o peso dos peixes, independente de qual é utilizado, uma vez que as medidas de comprimento são colineares. Além disso, é uma medida que por si parece ser um bom preditor do peso dos peixes.
Algumas observações, relativas a determinadas espécies de peixes, representam pontos aberrantes e comprometem a qualidade da regressão, como foi visto quando computando valores de distância de cook. Além disso, a quantidade de observações por espécie de peixe varia bastante, com diversas espécies com número baixo de observações, fator que deve ser levado em consideração na implementação do modelo.
- Posted on:
- January 1, 0001
- Length:
- 9 minute read, 1868 words
- Categories:
- Regressão linear Distância de Cook vif
- See Also: